This calculator can be used to expand and simplify any polynomial expression9 Mention any one web browser 10 What is DHTML?3 Give an example of nonlinear data structure 4 Name any one object oriented programming language 5 What is freestore?

Ml Aggarwal Solutions For Class 9 Chapter 3 Expansions Download Free Pdf
Expand (1/x y/3)^3 class 9
Expand (1/x y/3)^3 class 9-Class 10 Maths Basic vs Standard; Given an integer X, the task is to print the series and find the sum of the series Examples Input X = 2, N = 5 Output Sum = 31 1 2 4 8 16




Videos And Worksheets Corbettmaths
Class 6 Maths (with MCQs) Class 7 Maths (with MCQs) Class 8 Maths (with MCQs) Class 9 Maths (with MCQs) Class 10 Maths (with MCQs) Class 11 Maths (with MCQs) Class 12 Maths (with MCQs) NCERT Solutions Science;Expand each of the following, using suitable identities = 4 x 2 9 y 2 4 z 2 − 1 2 x y 1 2 y z class 9 Circles Coordinate Geometry What is Democracy?Solve limits stepbystep \square!
4 taylor approximation So e2 = 1 2 22 2!Expand 1 2 x 3 We pick the coefficients in the expansion from the row of Pascal's triangle (1,3,3,1) Powers of 2 x increase as we move left to right Any power of 1 is still 1 1 2 x 3 = 1(1)3 3(1)2 2 x 3(1)1 2 x 2 1 2 x 3 = 1 6 x 12 x2 8 x3 Exercises 2ML Aggarwal Solutions for Class 9 Maths Chapter 3 – Expansions are provided here to help students prepare and excel in their exams This chapter mainly deals with problems based on expansions Experts tutors have formulated the solutions in a step by step manner for students to grasp the concepts easily From the exam point of view, solving
Q10 Assertion The value of k for which the system of linear equations kxy=2 and 6x2y=3 has 2 ≠ b 1 /b 2 Answer Answer (d)Factorisation of Algebraic Expressions Exercise 52For example, x a, 2 x – 3y, 3 1 1 4, 7 5 x x x y − − , etc, are all binomial expressions 812 Binomial theorem If a and b are real numbers and n is a positive integer, then (a b) n =C 0 na n nC 1 an – 1 b1 C 2 Example 3 Find the 4th term from the end in the expansion of 3 9 2 2 2 x



1



Img1 Wsimg Com
The even root of a variable can be defined as x 1/2n, where n ∈ Z The value of y can be defined as y= 1sinx, or, y=1cosx, (since sinx ≤ 1 and cosx ≤1) Properties of Modulus Function Since the modulus function can be effective to find inequality between the numbers, here are the following properties of modulus function When a>0,Sample Papers Class 10 Solution Maths NewClass 10 Maths Basic vs Standard;




X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5 Cbsetuts Com
Example1 (1) Using the binomial series, find the first four terms of the expansion (2) Use your result from part (a) to approximate the value of Solution First, we will write the expansion formula for as follows Put value of n =\frac {1} {3}, till first four terms Thus expansion is (2) Now put x=02 in above expansion to get value of Plus One Maths Binomial Theorem Three Mark Questions and Answers Question 1 i) Here 7 is an odd number Therefore there are two middle terms and , ie;CBSE Sample Papers 2122 (Term 1) New;




Ex 2 5 6 Write The Following Cubes In Expanded Form I 2x 1 3




Leaving Certificate Pdf Free Download
Expand (− 2 x 5 y − 3 z) 2 using suitable identities Hard 1 6 x 2 4 y 2 9 z 2 1 6 x y 1 2 y z 2 4 x z Medium View solution > View more More From Chapter Polynomials View chapter > Practice more questions Easy Questions 2 Qs > class 9 Circles Coordinate Geometry What is Democracy?We know e0 = 1, so expand about c = 0 to get f(x) = ex = 1 1 (x 0) 1 2 (x 0)2 = 1 x x2 2! Polynomials Class 9 MCQs Questions with Answers Question 1 Question 2 Question 3 Find the value of 525² – 475² Question 4 Question 5 Question 6




Using Binomial Theorem Expand X Y 5 X Y 5 Dot And Hence Find The Value Of Sqrt 2 1 Youtube




Phase I Study Of A Multitargeted Recombinant Ad5 Psa Muc 1 Brachyury Based Immunotherapy Vaccine In Patients With Metastatic Castration Resistant Prostate Cancer Mcrpc Journal For Immunotherapy Of Cancer
A) x(x1)1 B) x(x 2 x1) C) x 2 (x1) D) x 2 (x1) E) x 2 (x1)1 Students who took this test also took Lesson the real number system Systems of Equations Elimination Solving systems of Davneet Singh is a graduate from Indian Institute of Technology, Kanpur He has been teaching from the past 10 years He provides courses for Maths and Science at Teachoo Question 5 Find the remainder when x 3 x 2 x 1 is divided by x – using remainder theorem Solution Let p (x) = x 3 x 2 x 1 and q (x) = x – Here, p (x) is divided by q (x) ∴ By using remainder theorem, we have Question 6 Find the common factor in the quadratic polynomials x 2 8x 15 and x 2 3x – 10




Expand Using Binomial Theorem 1 X 2 2 X 4 X 0 Mathematics Shaalaa Com




Binomial Expansion Binomial Expansions Copyright C By Houghton Mifflin Company Inc All Rights Reserved 2 The Binomial Theorem Provides A Useful Method Ppt Download
State reasons for your answer Ans (i) 4x 2 – 3x 7 ⇒ 4x2 – 3x 7x° ∵ All the exponents of x are whole numbers ∴ 4x 2 – 3x 7 is a polynomial in one variable (ii)Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us! MCQ Questions for Class 9 Maths Chapter 2 Polynomials with answers 1 Factorise 8a 3 b 3 12a2b 6ab 2 2 The value of k for which x 1 is a factor of the polynomial x3 x2 x k is 3 Using Remainder Theorem find the remainder when x3 x2 x 1 is divided by x




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5 Cbsetuts Com




Selina Mathematics Class 9th Solutions Icse Chapter 4 Expansion
2(xy) – 9(xy) 5 Solution 2(xy) – 9(xy) 5 Factorisation of Algebraic Expressions RD Sharma Class 9 Solutions Chapter 5 Exercise51 Factorisation of Algebraic Expressions RD Sharma Class 9 Solutions Chapter 5 Exercise51 Q 1 Factorisation of Algebraic Expressions Exercise 51;The properties of logarithms formulas that are applied for logarithmic calculations are given below 1 x m = a ⇒ log x a = m 2 log a 1 = 0 3 log a a = 1 4 log a ( x y) = log a x log a y 5 log a x y = log a x – log a y 6 log a ( x m) = m log a x 7 log a x = log c x log c a 8 a log1 Which of the following expressions are polynomials in one variable and which are not?




Expand 1x Y3 3 Maths Questions
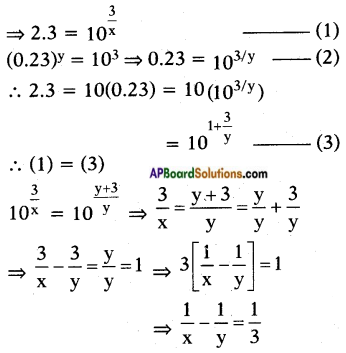



Ap Ssc 10th Class Maths Solutions Chapter 1 Real Numbers Ex 1 5 Ap Board Solutions
Explanation (x −y)3 = (x − y)(x −y)(x −y) Expand the first two brackets (x −y)(x − y) = x2 −xy −xy y2 ⇒ x2 y2 − 2xy Multiply the result by the last two brackets (x2 y2 −2xy)(x − y) = x3 − x2y xy2 − y3 −2x2y 2xy2 ⇒ x3 −y3 − 3x2y 3xy2 Always expand each term in the bracket by all the other32 Sympy Symbolic Mathematics in Python ¶ Author Fabian Pedregosa Objectives Evaluate expressions with arbitrary precision Perform algebraic manipulations on symbolic expressions Perform basic calculus tasks (limits, differentiation and integration) with symbolic expressions Solve polynomial and transcendental equations Maharashtra Board Class 8 Maths Chapter 5 Expansion Formulae Practice Set 51 Intext Questions and Activities Question 1 Use the above



Cbse 9 Math Cbse Polynomials Ncert Solutions




Amazon Com Pokemon Tcg 3 Booster Packs 30 Cards Total Value Pack Includes 3 Blister Packs Of Random Cards 100 Authentic Branded Pokemon Expansion Packs Random Chance At Rares Holofoils Toys Games
Class 6 Maths (with MCQs) Class 7 Maths (with MCQs) Class 8 Maths (with MCQs) Class 9 Maths (with MCQs) Class 10 Maths (with MCQs) Class 11 Maths (with MCQs) Class 12 Maths (with MCQs) NCERT Solutions Science; Assertion and Reason Questions for Class 9 Maths Chapter 3 Coordinate Geometry Directions In the following questions, a statement of assertion (A) is followed by a statement of reason (R)Mark the correct choice as (a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A) Therefore in the given equation will become x (y z) =xy xz We hope the simplification of brackets is clear to you know Let us look at some complex examples for a better understanding Example 1 Expand and simplify 9 (5 3) Solution In question 9 (5 3) let us use the Distributive Property a (b c) = ab bc 9 (5 3) = 9 × 5 9 × 3




Ks3 And Ks4 Factorising Worksheets Cazoom Maths Worksheets
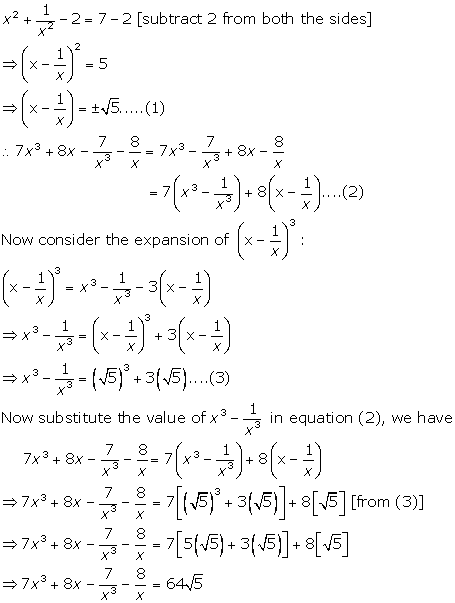



Chapter 4 Expansion Selina Concise Mathematics Part I Solutions For Class 9 Mathematics Icse Topperlearning
Assertion and Reason Questions for Class 10 Maths Chapter 8 Introduction to Trigonometry Directions In the following questions, a statement of assertion (A) is followed by a statement of reason (R)Mark the correct choice as (a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A) Give possible expressions for the length and breadth of each of the following rectangles, in which their areas are given (i) Area 25a2 – 35a 12 (ii) Area 35y2 13y – 12 Solution (i) We have, area of rectangle = 25a 2 – 35a12 = 25a 2 – a – 15a12All those who say programming isn't for kids, just haven't met the right mentors yet Join the Demo Class for First Step to Coding Course, specifically designed for students of class 8 to 12 The students will get to learn more about the world of programming in these free classes which will definitely help them in making a wise career choice in the future



Expand 1 X Y 3 Whole Cube Studyrankersonline



2
Transcript Ex , 6 Find the 13th term in the expansion of ("9x – " 1/(3√x))^18 , x ≠ 0 We know that General term of expansion (a b)n is Tr 1 = nCr an – r br We need to calculate 13th term (ie T13 = T121 ) of expansion ("9x – " 1/(3√x))^18 Putting r = 12 , n = 18 , a = 9x & b = 1/(3√x) T12 1 = 18C12 (9x)18 – 12 ((−1)/(3√x))^12 = 18!/(12!(18 − 12)) (9x)6 ×But we can't evaluate an infinite series, so we truncate Taylor Series Polynomial Approximation The Taylor Polynomial of degree n for the function f(x) about the pointEx 25 Class 9 Maths Question 3 Factorise the following using appropriate identities (i) 9x 2 6xy y 2 (ii) 4y 2 – 4y 1 (iii) x 2 – Solution Ex 25 Class 9 Maths Question 4 Expand each of the following, using suitable identities (i) (x 2y 4z) 2 (ii) (2x y z) 2 (iii) (2x 3y 2z) 2 (iv) (3a – 7b c) 2 (v) (2x 5y




Expand 1 3 X 2 3 Y Whole Cube Brainly In




Exponent Rules 7 Key Strategies To Solve Tough Equations Prodigy Education
4 th and 5 th terms in the above expansion ii) Here 10 is an even number Therefore middle terms term in the above expansion iii) Here 17 is an odd number Mathematics Class 9th Chapter 5 Solution 1 Instructor Adil Aslam Email adilaslam5959@gmailcom Notes By Adil Aslam Education MSCS Mathematics Class 9th Chapter No 5 Factorization Factorization If a polynomial 𝑝 (𝑥) can be expressed as 𝑝 (𝑥) = 𝑔 (𝑥) ℎ (𝑥), then each of the polynomials 𝑔 (𝑥) and ℎ (𝑥) isAlgebra formulas for class 9 include formulas related to algebra identities or expressions Algebraic identities chapter is introduced in CBSE class 9 This is a tricky chapter where one needs to learn all the formula and apply them accordingly To make it easy for them, BYJU'S provide all the formulas on a single page ( x^{3} y^{3




The Coefficient Of X 3y 4z In The Expansion Of 1 X Y Z 9 Is A 2 9c 7 7c 4 B 2 9c 2 7c 4 C 9c 7 7c 4 D None Of These




Properties Of Logarithms Circuit Activity High School Math Calculus Teacher High School Mathematics
PARTB Answer any five questions Each question carries two marks 11 Prove algebraically X3 Mid point formula 1 2 1 2 x x y y, 2 2 4 Centriod formula 1 2 3 1 2 3 x x x y y y, 3 3 5 Area of triangle when their vertices are given,Sample Papers Class 10 Solution Maths New




Section 8 5 The Binomial Theorem Ppt Download




Section 8 5 The Binomial Theorem Ppt Download
To generate Pascal's Triangle, we start by writing a 1 In the row below, row 2, we write two 1's In the 3 rd row, flank the ends of the rows with 1's, and add latex11/latex to find the middle number, 2 In the latexn\text{th}/latex row, flank the ends of the row with 1's (2x3y)^3=8x^336x^2y54xy^227y^3 Using Binomial theorem expansion, (xy)^3=x^33x^2y3xy^2y^3 Hence (2x3y)^3 = (2x)^33(2x)^2*3y3(2x)(3y)^2(3y)^3 = 8x^33*4x^2*3y3*2x*9y^227y^3 = 8x^336x^2y54xy^227y^3 Algebra Science Anatomy & Physiology AstronomySelina Solutions for Class 9 Maths Chapter 4 Expansions The Chapter 4, Expansions, contains 5 exercises and the Solutions given here contains the answers for all the questions present in these exercises Let us have a look at some of the topics that are being discussed in this chapter 41 Introduction 42 Identities




Spatial Zoning For Better Structural Topology Design And Performance Sciencedirect



How To Expand The Binomial X Y 10 Quora
CBSE Sample Papers 2122 (Term 1) New; ML Aggarwal Class 9 Solutions for ICSE Maths Chapter 3 Expansions Chapter Test Question 1 Find the expansions of the following (i) (2x 3y 5) (2x 3y – 5) (ii) (6 – 4a 7b) 2 (iii) (7 – 3xy) 3 (iv) (x y 2) 3NCERT Solutions Class 9 Maths Chapter 1 Number Systems Exercise 13 are provided here which are prepared by our subject experts which makes it easy for students to learn The students use it for reference while solving the exercise problems The third exercise in Number Systems Exercise 13 discusses real numbers and their decimal Expansion




Expansions Popular Questions Icse Class 9 Math Mathematics Meritnation




Mathematiques Expression A 4x 1 7 2x
6 Define a tuple 7 Expand FTP 8 What is a simplex communication mode?The Binomial Expansion Theorem is an algebra formula that describes the algebraic expansion of powers of a binomial According to the binomial expansion theorem, it is possible to expand any power of x y into a sum of the termsSelina Concise Mathematics Part I Solutions for Class 9 Mathematics ICSE, 4 Expansion All the solutions of Expansion Mathematics explained in detail by experts to help students prepare for their ICSE exams x 3 y 3 = 1331 72(11) = 1331 792 = 539 So, sum of their cubes is 539 Question 16 If 4x 2 y 2 = a and xy = b, find the




Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 5 Polynomials




9 5 The Binomial Theorem Let S Look At The Expansion Of X Y N Ppt Video Online Download
Nazism and the Rise of Hitler Socialism in Europe and the Russian Revolution class 10So the answer is 3 3 3 × (3 2 × x) 3 × (x 2 × 3) x 3 (we are replacing a by 3 and b by x in the expansion of (a b) 3 above) Generally It is, of course, often impractical to write out Pascal"s triangle every time, when all that we need to know are the entries on the nth line Clearly, the first number on the nth line is 1 The Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 34 Question 1 Expand the following (i) (2x 3y 4z) 2 (ii) (p 2q 3r) 2 (x \(\frac{1}{y}\)) 3 Solution (i) (3a – 4b) 3 We know that Solved English Grammar



2
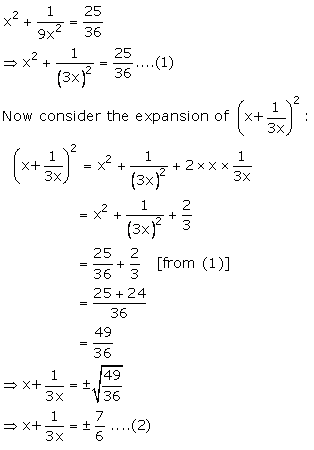



Chapter 4 Expansion Selina Concise Mathematics Part I Solutions For Class 9 Mathematics Icse Topperlearning
Solution (i) The example of monomial of degree 1 is 5y or 10x (ii) The example of binomial of degree is 6x x 11 or x 1 (iii) The example of trinomial of degree 2 is x 2 – 5x 4 or 2x 2 x1 Question 7 Find the value of the polynomial 3x 3 – Example 7 Find the coefficient of x6y3 in the expansion of (x 2y)9 We know that General term of expansion (a b)n is Tr1 = nCr an–r br For (x 2y)9, Putting n = 9 , a = x , b = 2y Tr 1 = 9Cr (x)9 – r (2y)r = 9Cr (x)9 – r (y)r (2)r We need to find coefficient of x6 y3 Comparing yr = y3 r = 3 Putting r = 3 in (1) T31 = 9C3 x9




Expand X 2 2y 5 Using Binomial Expansion Youtube




Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9




Please Expand 1 X Y 3 Whole Cube Brainly In



Cbse 9 Math Cbse Polynomials Ncert Solutions



2
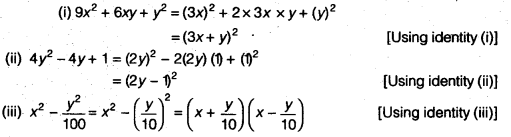



Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5
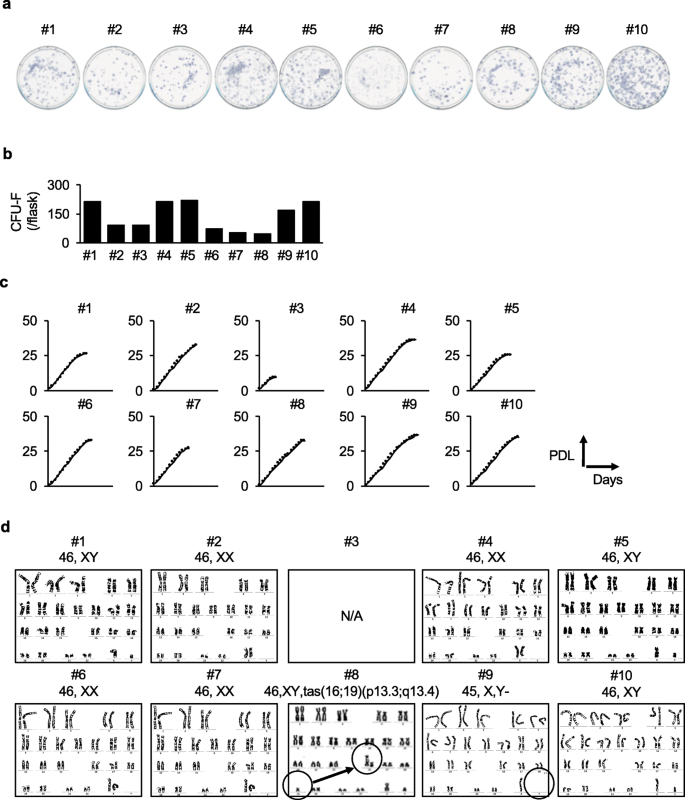



A Model Study For The Manufacture And Validation Of Clinical Grade Deciduous Dental Pulp Stem Cells For Chronic Liver Fibrosis Treatment Stem Cell Research Therapy Full Text



Packs Expand Your Ableton Studio With Instruments Sounds Ableton




Selina Solutions For Concise Mathematics Class 9 Icse Chapter 4 Expansions Including Substitution Latest Edition Shaalaa Com




Interactive Programming For Parametric Cad Mathur Computer Graphics Forum Wiley Online Library




Selina Concise Mathematics Class 9 Icse Solutions For Chapter 3 Expansions
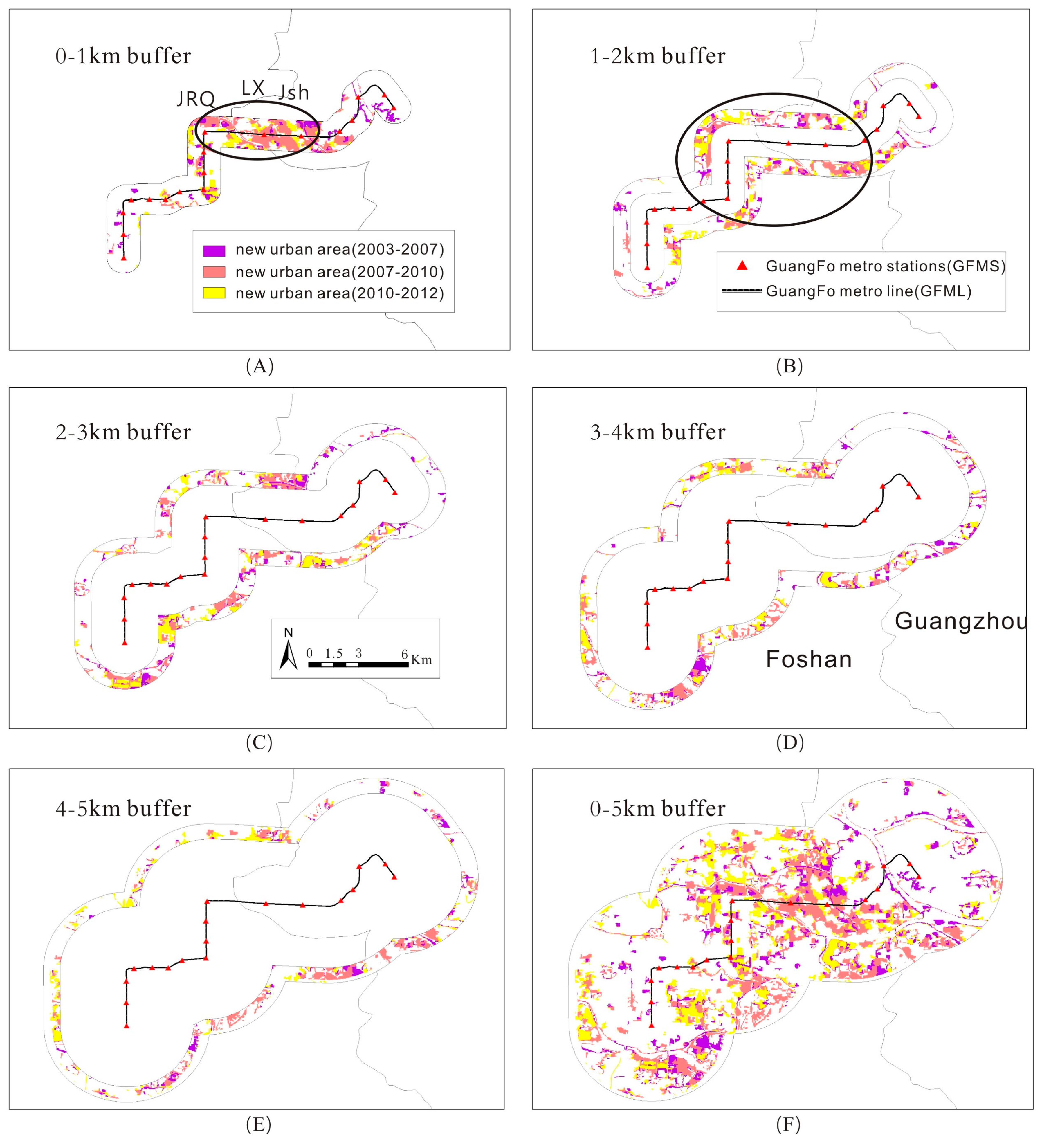



Sustainability Free Full Text Spatial And Temporal Dynamics Of Urban Expansion Along The Guangzhou Foshan Inter City Rail Transit Corridor China Html




Ncert Solutions Class 9 Maths Chapter 2 Exercise 2 4 Polynomials



Wssd Org




Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 5 Polynomials




Ml Aggarwal Class 9 Solutions For Icse Maths Chapter 3 Expansions Chapter Test A Plus Topper




1 X Y 3 3 Expand Brainly In




Ml Aggarwal Icse Solutions For Class 9 Maths Ch 3 Expansions A Plus Topper



What Is The Answer Of X Y Quora




ベスト X5 Y5 Expand シモネタ




Taylor Series Wikipedia
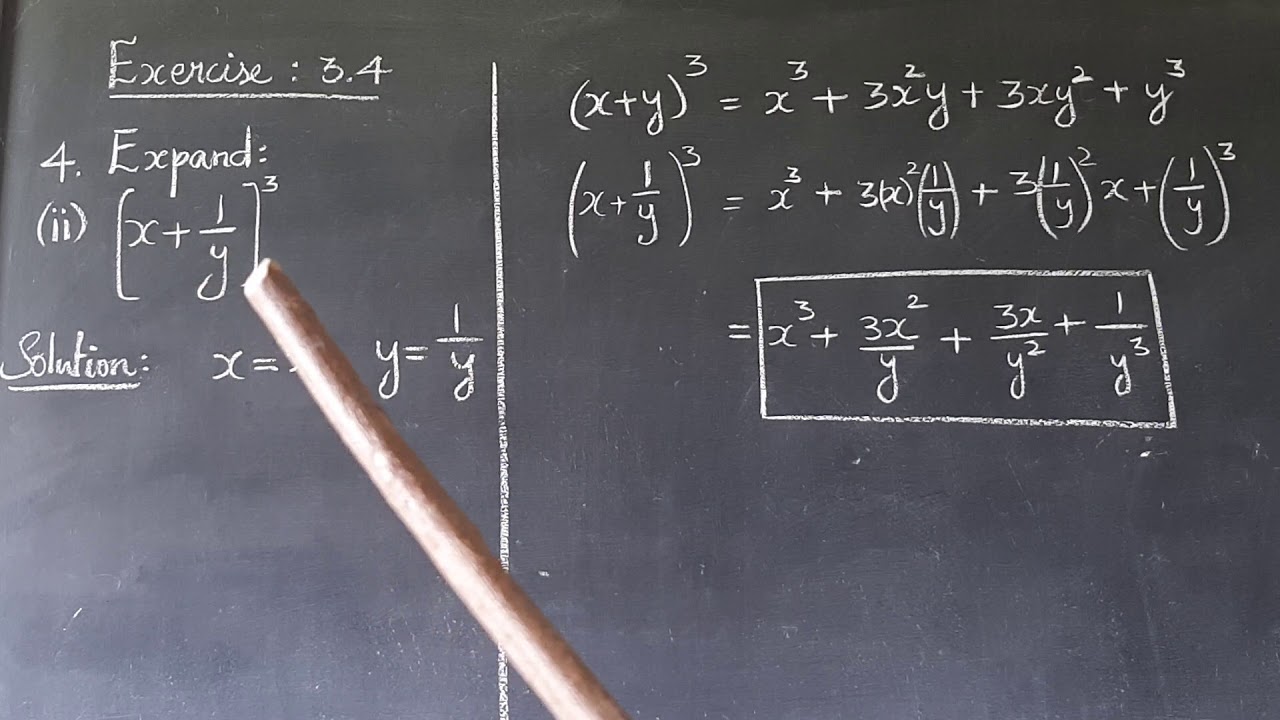



Std 9 Expand X 1 Y Youtube




Expand The Following I 3a 2b 3 Ii 1 X Y 3 3 Iii 4 1 3x 2




Expand Each Of The Following Using Suitable Identities 2x 3y 2z 2



Cbse 9 Math Cbse Polynomials Ncert Solutions




Ml Aggarwal Solutions For Class 9 Chapter 3 Expansions Download Free Pdf



2




Ncert Solutions For Class 11 Maths Chapter 8 Binomial Theorem




Ncert Solutions For Class 11 Maths Chapter 8 Binomial Theorem Free Pdf
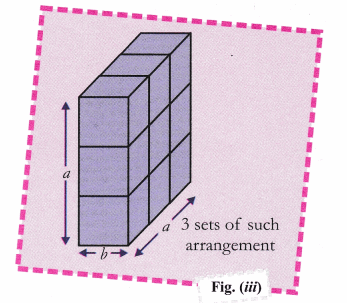



Cbse Class 9 Maths Lab Manual Algebraic Identity A B 3 A3 3a2b 3ab2 Cbse Sample Papers




Expansions Popular Questions Icse Class 9 Math Mathematics Meritnation



Rename Markers In Logic Pro الدعم Apple




Example 22 I Write The Cubes In Expanded Form 3a 4b 3




Expanding Binomials Video Series Khan Academy




ベスト X5 Y5 Expand シモネタ




Expand 1 X Y 3 3 Solve It Fastly Brainly In




Expand The Following I 3a 2b 3 Ii 1 X Y 3 3 Iii 4 1 3x 2



1
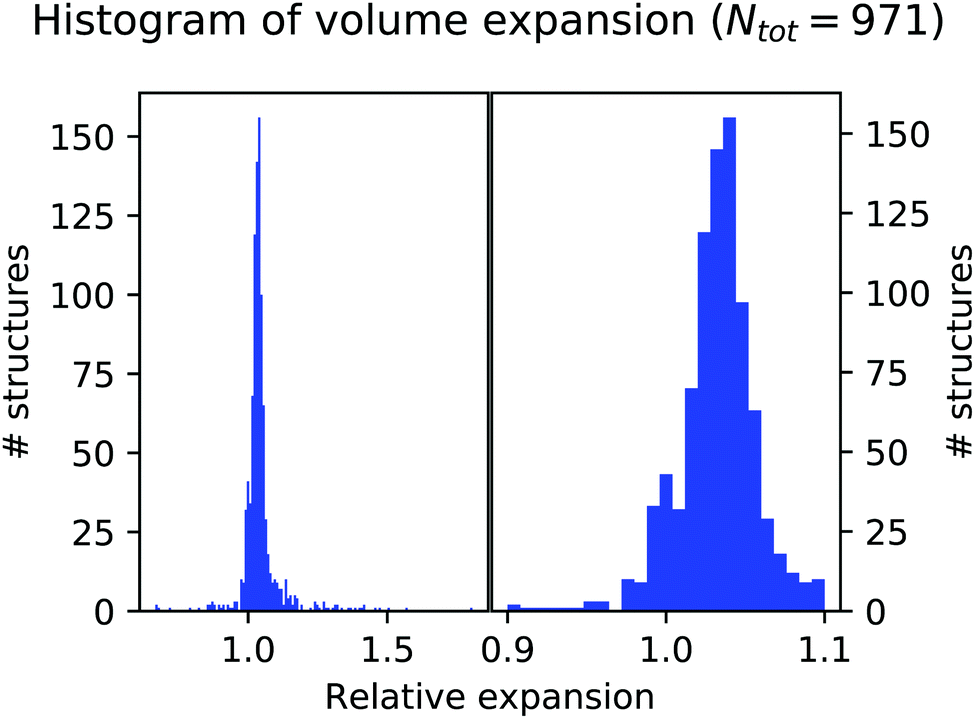



High Throughput Computational Screening For Solid State Li Ion Conductors Energy Environmental Science Rsc Publishing



2




Binomial Theorem Wikipedia




The Coefficient Of X 10 In The Expansion Of 1 X 2 1 X 2 3 1 X 3 4 Is Equal To




Binomial Expansion Formulas Derivation Examples




Videos And Worksheets Corbettmaths




International Cancer Seminars A Focus On Esophageal Squamous Cell Carcinoma Annals Of Oncology
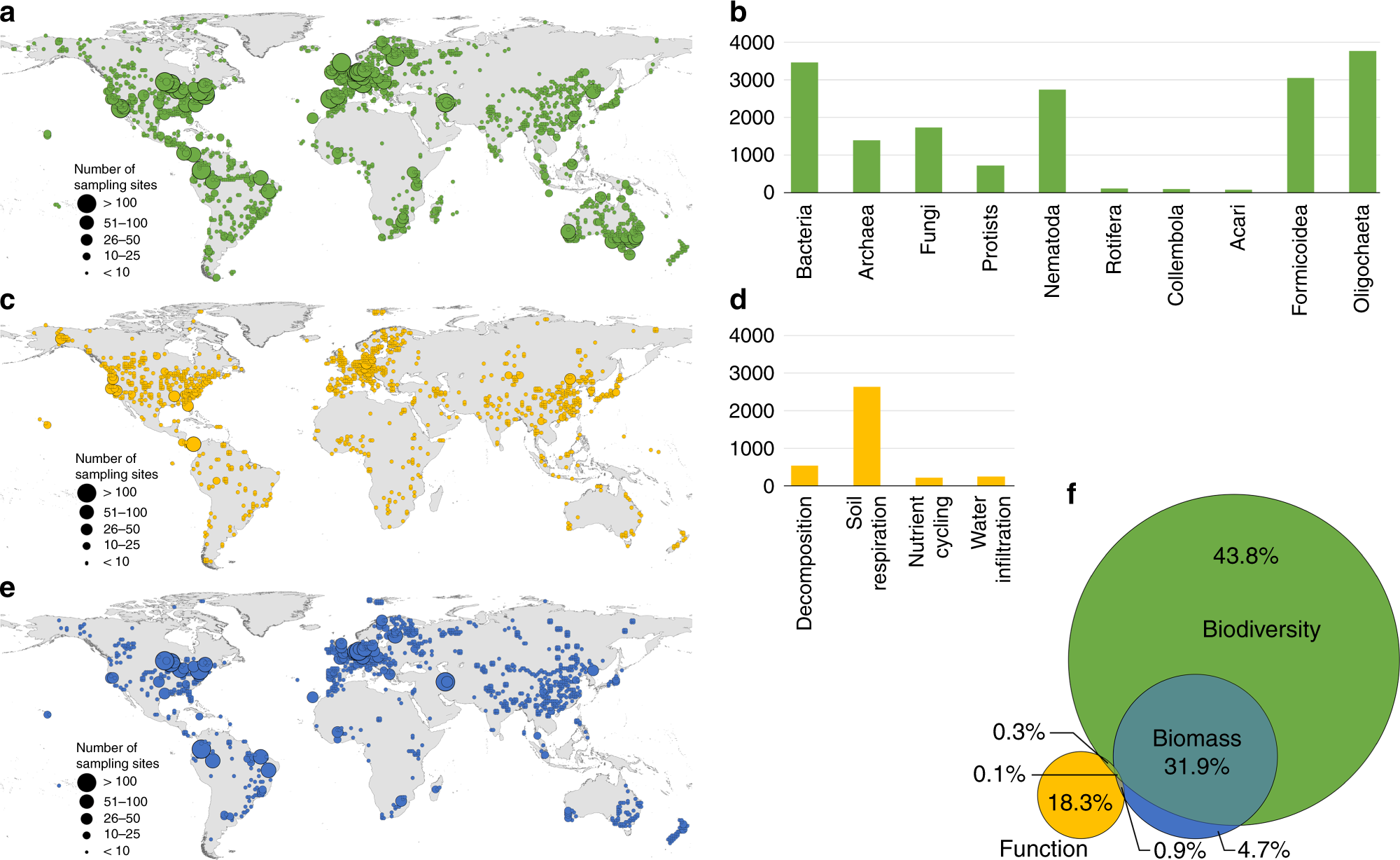



Blind Spots In Global Soil Biodiversity And Ecosystem Function Research Nature Communications




X Y 2 Expand Aoierrico



Expand Tan 1y X About The Point 1 1 Using Taylor S Theorem Up To The Second Degree Terms Sarthaks Econnect Largest Online Education Community
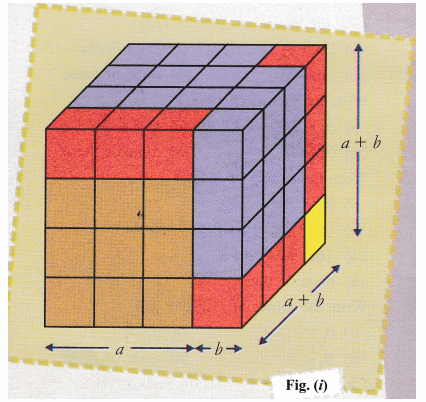



Cbse Class 9 Maths Lab Manual Algebraic Identity A B 3 A3 3a2b 3ab2 Cbse Sample Papers




Chapter 4 Expansion Selina Concise Mathematics Part I Solutions For Class 9 Mathematics Icse Topperlearning
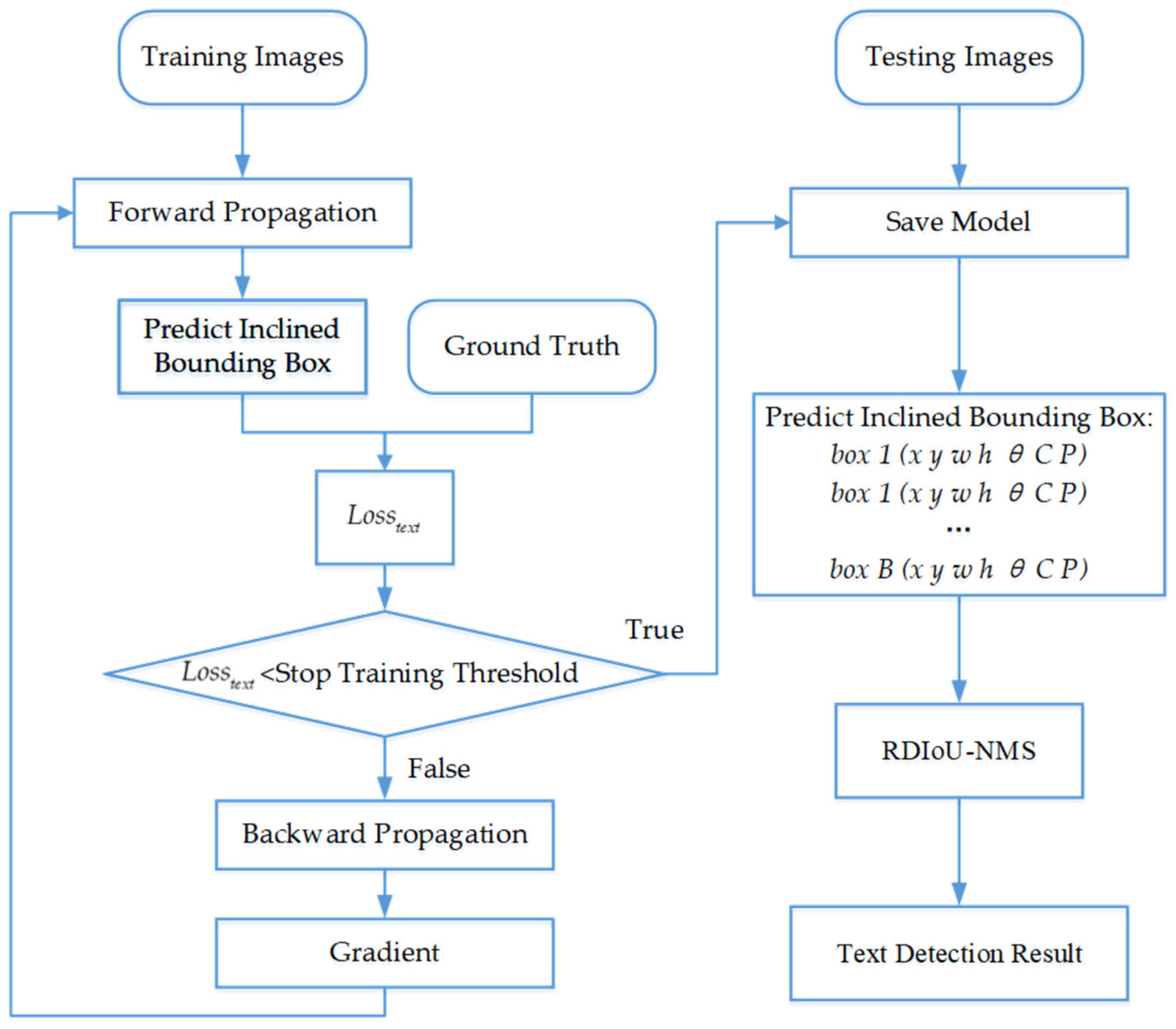



Sensors Free Full Text R Yolo A Real Time Text Detector For Natural Scenes With Arbitrary Rotation Html




Ml Aggarwal Icse Solutions For Class 9 Maths Ch 3 Expansions A Plus Topper




Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9
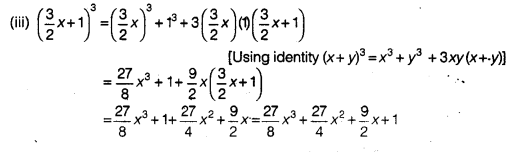



Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5




Find The Total Number Of Terms In The Expansion Of 1 1 X Y 10 And Cofficient Of X 2 Y 3




Algebra Formulas For Class 9 Pdf Download Free Here
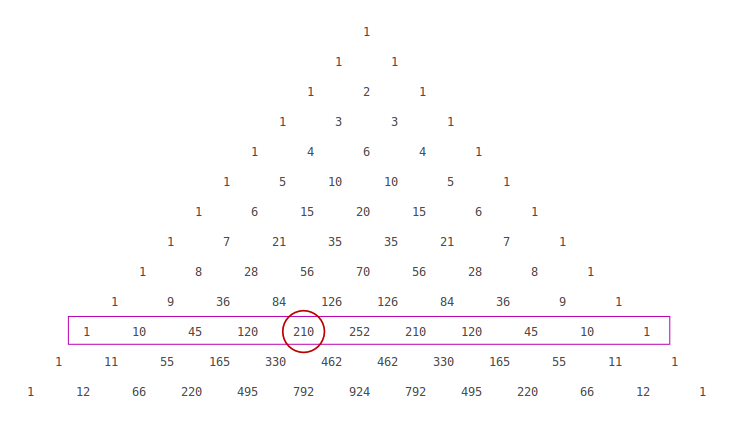



How Do You Find The Coefficient Of X 6 In The Expansion Of 2x 3 10 Socratic




X Y 2 Expand Aoierrico




Ncert Exemplar Class 9 Maths Solutions Chapter 2 Polynomials Cbse Tuts




Ex 8 2 8 Find Middle Terms Of X 3 9y 10 Binomial



Expand Tan 1y X About The Point 1 1 Using Taylor S Theorem Up To The Second Degree Terms Sarthaks Econnect Largest Online Education Community
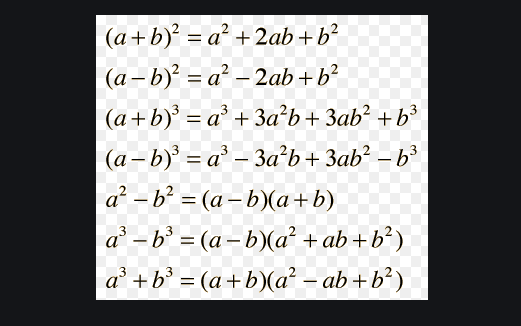



Expansions Ml Aggarwal Icse Class 9 Maths Solutions Icsehelp
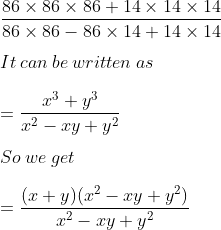



Ml Aggarwal Solutions For Class 9 Chapter 3 Expansions Download Free Pdf




Ncert Solutions For Class 8 Maths Ch 14 Factorization Exercise 14 2
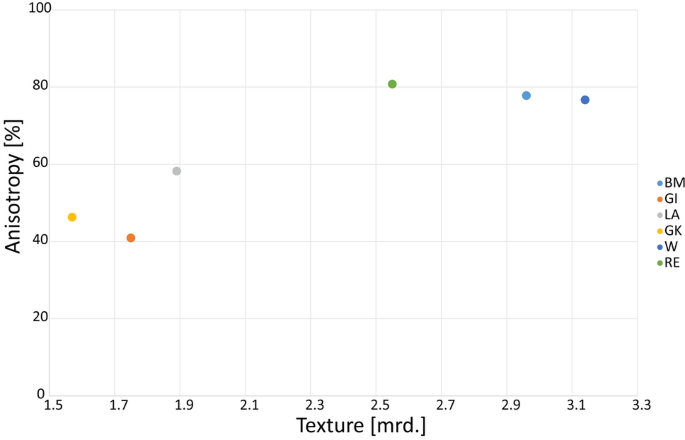



Marble Decay Towards A Measure Of Marble Degradation Based On Ultrasonic Wave Velocities And Thermal Expansion Data Springerlink




Please Expand 1 X Y 3 Whole Cube Brainly In



Solve For X And Y X 2 2y 3 1 X Y 3 3 Sarthaks Econnect Largest Online Education Community




Ml Aggarwal Solutions For Class 9 Chapter 3 Expansions Download Free Pdf



0 件のコメント:
コメントを投稿